openSUSE:Libzypp satsolver internals
Internals
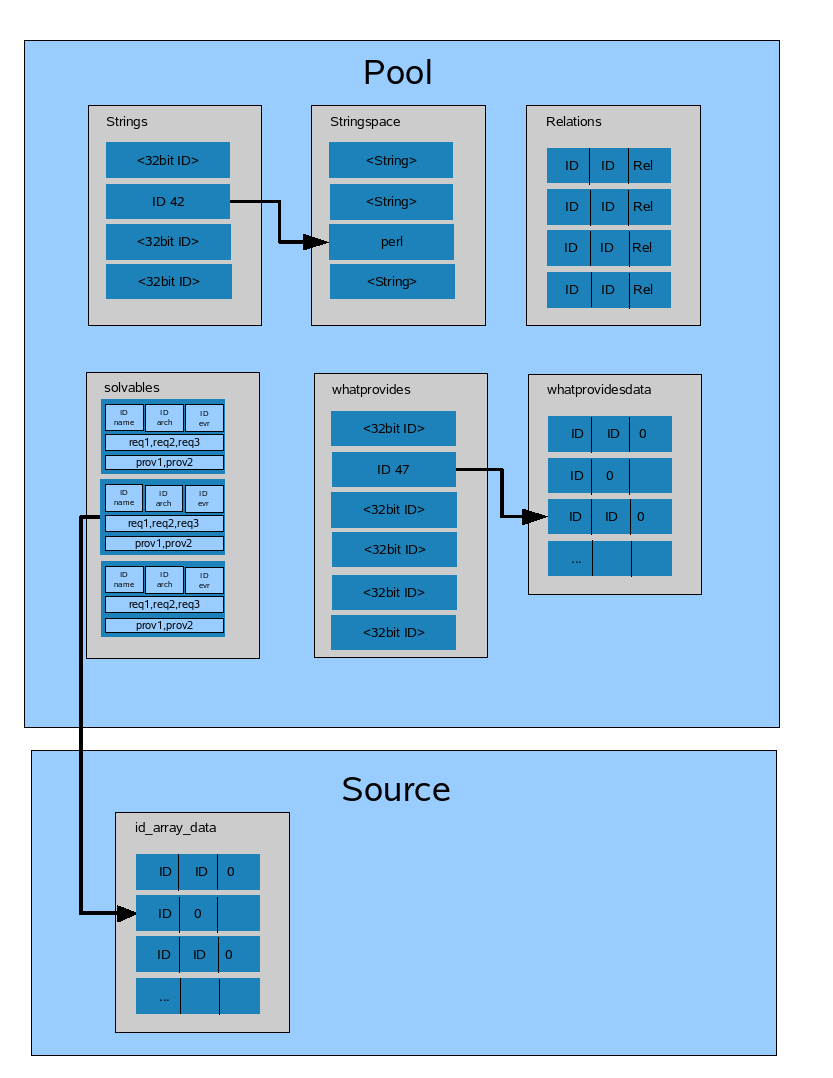
Pool and sources
Rules
Definition of a rule
There are some kind of rules:
- Direct Assertion: e.G. (A) = install A; (-A) = remove A
- Binary Rule: e.G. (!A|B) = A requires B
- Rules with more than 2 possibilities: (!A|B1|B2 ) = A requires B1 OR B2
A rule contains a single literal (called p) and a pointer on an array of literals (called d). Here some examples:
p = direct literal; always < 0 for installed rpm rules
d, if < 0 direct literal, if > 0 offset into whatprovides, if == 0 rule is assertion (look at p only)
- Install: p > 0, d = 0 (A) user requested install
- Remove: p < 0, d = 0 (-A) user requested remove
- Requires: p < 0, d > 0 (-A|B1|B2|...) d: <list of providers for requirement of p>
- Updates: p > 0, d > 0 (A|B1|B2|...) d: <list of updates for solvable p>
- Conflicts: p < 0, d < 0 (-A|-B) either p (conflict issuer) or d (conflict provider) (binary rule)
- No-op ?: p = 0, d = 0 (null) (used as policy rule placeholder)
Rule array
Rules are stored in an array. Additional the rules are grouped in the array:
| rpm rules of involved packages |
| job rules |
| installed solvable rules (installed rule) |
| weak rules (i.e. rules that get autodisabled if unsolvable) |
| learnt rules |
Most groups have defined offsets variables:
solv->learntrules
solv->weakrules
solv->systemrules
solv->jobrules
The length of this array is defined by:
solve->nrules
Jobs
Jobs are stored in a job queue. Each job has two elements:
- how :
- SOLVER_INSTALL_SOLVABLE
- SOLVER_ERASE_SOLVABLE
- SOLVER_INSTALL_SOLVABLE_NAME
- SOLVER_ERASE_SOLVABLE_NAME
- SOLVER_INSTALL_SOLVABLE_PROVIDES
- SOLVER_ERASE_SOLVABLE_PROVIDES
- SOLVER_INSTALL_SOLVABLE_UPDATE
- what :
- id of solvables OR
- id of provided string OR
- id of dependency
Watch array
The watch array will be generated before the solver starts solving and will be updated while a solver run. Watches get triggered when the corresponding literal goes False. As there are positive and negative literals we need nsolvables*2 entries. Each entry is a linked list through all of the involved rules.
The information how the watch array will be built is taken from each rule. A rule has two defined watchpoints (w1,w2) which depends on the kind of rule:
- Direct assertion (no watch needed)( if d <0 ) --> d = 0, w1 = p, w2 = 0
- Binary rule: p = first literal, d = 0, w2 = second literal, w1 = p
- Every other : w1 = p, w2 = whatprovidesdata[d];
- Disabled rule: w1 = 0
( p and d are explained in the rule definition chapter)
The watch array has nsolvables*2 entries and is addressed from the middle
- middle-solvable : decision to conflict, offset point to linked-list of rules
- middle+solvable : decision to install: offset point to linked-list of rules
So the index is the solvable ID (negativ or positiv) and the value will be the concerning watchpoint of a rule. For each rule these watchpoint will be regarded in the watch array:
static void
addwatches(Solver *solv, Rule *rule)
{
int nsolvables = solv->pool->nsolvables;
rule->n1 = solv->watches[nsolvables + rule->w1];
solv->watches[nsolvables + rule->w1] = rule - solv->rules;
rule->n2 = solv->watches[nsolvables + rule->w2];
solv->watches[nsolvables + rule->w2] = rule - solv->rules;
}
An already defined watchpoint will be stored in n1 or n2 of the concerning rule before it will be overwritten by the new watchpoint.
Decisions
Decisions are stored in 3 different queues/maps.
decisionq
Is a queue of solvables IDs and reflects the state which solvable will be installed(positiv ID) or will be deleted(negativ ID).
The length of this queue will be stored in decisionq.count .
decisionmap
The index is the ID of the concerning solvable. The value reflects the decision level of installation(positiv) or conflict(negativ).
decisionq_why
Is a queue of rule IDs that corresponds to the decisionq. This queue saves the reason why the solver made the decision. A reason is either a rule index if the decision was made because of a rule going unit, or "0".
The value can be "0" if:
- The concerning solvable is the SYSTEMRESOLVABLE, which is always installed.
- The decision is a rpm rule assertion only. We do not create rules for those.
- The decision was done by arbitrary choice.
The length of this queue will be stored in decisionq_why.count .
How does the SAT solver work
The best way to get an overview about the solver workings would be to explain it with simple examples.
Best case (without problems)
Environment:
| Package | provides | requires | conflicts |
|---|---|---|---|
| A | a, foo | h | |
| B | b, foo | g | |
| C | c, foo | f | |
| D | d, foo | e | |
| E | e, bar | d | |
| F | f, bar | c | |
| G | g, bar | b | |
| H | h, bar | a | |
| Z | foo, bar |
Task:
| Package | action |
|---|---|
| A | install |
| B | install |
Building rules
Create rpm rules for packages involved with a job:
Rule #1: !Z-1.0-1.noarch [11] (w1) Install.level1 A-1.0-1.noarch [3] (w2) Install.level1 B-1.0-1.noarch [4] C-1.0-1.noarch [5] D-1.0-1.noarch [6] next rules: 0 0 Rule #2: !Z-1.0-1.noarch [11] (w1) Install.level1 E-1.0-1.noarch [7] (w2) F-1.0-1.noarch [8] G-1.0-1.noarch [9] H-1.0-1.noarch [10] next rules: 0 0 Rule #3: !H-1.0-1.noarch [10] (w1) !A-1.0-1.noarch [3] (w2) Install.level1 next rules: 0 0 Rule #4: !G-1.0-1.noarch [9] (w1) !B-1.0-1.noarch [4] (w2) next rules: 0 0 Rule #5: !F-1.0-1.noarch [8] (w1) !C-1.0-1.noarch [5] (w2) next rules: 0 0 Rule #6: !E-1.0-1.noarch [7] (w1) !D-1.0-1.noarch [6] (w2) next rules: 0 0
Creating job rules:
Rule #7: A-1.0-1.noarch [3] (w1) Install.level1 next rules: 0 0 Rule #8: Z-1.0-1.noarch [11] (w1) Install.level1 next rules: 0 0
Initial decision
Initial decisions will be taken by generating the rules. These decisions (descibed in the queue decisionq and the map decisionmap) have 0 entries in the queue decisionq_why.
----- Decisions ----- SYSTEMSOLVABLE install A-1.0-1.noarch install Z-1.0-1.noarch ----- Decisions end -----
Solving
Propagate a decision
For each decision in the decisionq the propagate algorithm will be called. There will be checked the watch list if this decision hits another rule for this rule additional decisions will be made:
----- propagate ----- popagate for decision 1 level 1 system:system-.noarch [1] Install.level1 Watches: solvable [-12] -- rule [0] solvable [-11] -- rule [1] solvable [-10] -- rule [3] solvable [-9] -- rule [4] solvable [-8] -- rule [5] solvable [-7] -- rule [6] solvable [-6] -- rule [6] solvable [-5] -- rule [5] solvable [-4] -- rule [4] solvable [-3] -- rule [3] solvable [-2] -- rule [0] solvable [-1] -- rule [0] solvable [0] -- rule [0] solvable [1] -- rule [0] solvable [2] -- rule [0] solvable [3] -- rule [1] solvable [4] -- rule [0] solvable [5] -- rule [0] solvable [6] -- rule [0] solvable [7] -- rule [2] solvable [8] -- rule [0] solvable [9] -- rule [0] solvable [10] -- rule [0] solvable [11] -- rule [0] solvable [12] -- rule [0] popagate for decision 3 level 1 A-1.0-1.noarch [3] Install.level1 Watches: solvable [-12] -- rule [0] solvable [-11] -- rule [1] solvable [-10] -- rule [3] solvable [-9] -- rule [4] solvable [-8] -- rule [5] solvable [-7] -- rule [6] solvable [-6] -- rule [6] solvable [-5] -- rule [5] solvable [-4] -- rule [4] solvable [-3] -- rule [3] solvable [-2] -- rule [0] solvable [-1] -- rule [0] solvable [0] -- rule [0] solvable [1] -- rule [0] solvable [2] -- rule [0] solvable [3] -- rule [1] solvable [4] -- rule [0] solvable [5] -- rule [0] solvable [6] -- rule [0] solvable [7] -- rule [2] solvable [8] -- rule [0] solvable [9] -- rule [0] solvable [10] -- rule [0] solvable [11] -- rule [0] solvable [12] -- rule [0] watch triggered Rule #3: !H-1.0-1.noarch [10] (w1) !A-1.0-1.noarch [3] (w2) Install.level1 next rules: 0 0 unit Rule #3: !H-1.0-1.noarch [10] (w1) !A-1.0-1.noarch [3] (w2) Install.level1 next rules: 0 0 -> decided to conflict H-1.0-1.noarch popagate for decision 11 level 1 Z-1.0-1.noarch [11] Install.level1 Watches: solvable [-12] -- rule [0] solvable [-11] -- rule [1] solvable [-10] -- rule [3] solvable [-9] -- rule [4] solvable [-8] -- rule [5] solvable [-7] -- rule [6] solvable [-6] -- rule [6] solvable [-5] -- rule [5] solvable [-4] -- rule [4] solvable [-3] -- rule [3] solvable [-2] -- rule [0] solvable [-1] -- rule [0] solvable [0] -- rule [0] solvable [1] -- rule [0] solvable [2] -- rule [0] solvable [3] -- rule [1] solvable [4] -- rule [0] solvable [5] -- rule [0] solvable [6] -- rule [0] solvable [7] -- rule [2] solvable [8] -- rule [0] solvable [9] -- rule [0] solvable [10] -- rule [0] solvable [11] -- rule [0] solvable [12] -- rule [0] watch triggered Rule #1: !Z-1.0-1.noarch [11] (w1) Install.level1 A-1.0-1.noarch [3] (w2) Install.level1 B-1.0-1.noarch [4] C-1.0-1.noarch [5] D-1.0-1.noarch [6] next rules: 2 0 watch triggered Rule #2: !Z-1.0-1.noarch [11] (w1) Install.level1 E-1.0-1.noarch [7] (w2) F-1.0-1.noarch [8] G-1.0-1.noarch [9] H-1.0-1.noarch [10] Conflict.level1 next rules: 0 0 -> move w1 to F-1.0-1.noarch popagate for decision -10 level 1 !H-1.0-1.noarch [10] Conflict.level1 Watches: solvable [-12] -- rule [0] solvable [-11] -- rule [1] solvable [-10] -- rule [3] solvable [-9] -- rule [4] solvable [-8] -- rule [5] solvable [-7] -- rule [6] solvable [-6] -- rule [6] solvable [-5] -- rule [5] solvable [-4] -- rule [4] solvable [-3] -- rule [3] solvable [-2] -- rule [0] solvable [-1] -- rule [0] solvable [0] -- rule [0] solvable [1] -- rule [0] solvable [2] -- rule [0] solvable [3] -- rule [1] solvable [4] -- rule [0] solvable [5] -- rule [0] solvable [6] -- rule [0] solvable [7] -- rule [2] solvable [8] -- rule [2] solvable [9] -- rule [0] solvable [10] -- rule [0] solvable [11] -- rule [0] solvable [12] -- rule [0] ----- propagate end-----
Handle unfulfilled rules
Evaluate unfulfilled rules
Has to be described. I have still not understand.
Make decisions for unfulfilled rules
deciding unresolved rules unfulfilled Rule #2: !Z-1.0-1.noarch [11] Install.level1 E-1.0-1.noarch [7] (w2) F-1.0-1.noarch [8] (w1) G-1.0-1.noarch [9] H-1.0-1.noarch [10] Conflict.level1 next rules: 0 0 prune_to_best_version 3 - E-1.0-1.noarch - F-1.0-1.noarch - G-1.0-1.noarch installing E-1.0-1.noarch
Propagate new decisions
----- propagate ----- popagate for decision 7 level 2 E-1.0-1.noarch [7] Install.level2 Watches: solvable [-12] -- rule [0] solvable [-11] -- rule [1] solvable [-10] -- rule [3] solvable [-9] -- rule [4] solvable [-8] -- rule [5] solvable [-7] -- rule [6] solvable [-6] -- rule [6] solvable [-5] -- rule [5] solvable [-4] -- rule [4] solvable [-3] -- rule [3] solvable [-2] -- rule [0] solvable [-1] -- rule [0] solvable [0] -- rule [0] solvable [1] -- rule [0] solvable [2] -- rule [0] solvable [3] -- rule [1] solvable [4] -- rule [0] solvable [5] -- rule [0] solvable [6] -- rule [0] solvable [7] -- rule [2] solvable [8] -- rule [2] solvable [9] -- rule [0] solvable [10] -- rule [0] solvable [11] -- rule [0] solvable [12] -- rule [0] watch triggered Rule #6: !E-1.0-1.noarch [7] (w1) Install.level2 !D-1.0-1.noarch [6] (w2) next rules: 0 0 unit Rule #6: !E-1.0-1.noarch [7] (w1) Install.level2 !D-1.0-1.noarch [6] (w2) next rules: 0 0 -> decided to conflict D-1.0-1.noarch popagate for decision -6 level 2 !D-1.0-1.noarch [6] Conflict.level2 Watches: solvable [-12] -- rule [0] solvable [-11] -- rule [1] solvable [-10] -- rule [3] solvable [-9] -- rule [4] solvable [-8] -- rule [5] solvable [-7] -- rule [6] solvable [-6] -- rule [6] solvable [-5] -- rule [5] solvable [-4] -- rule [4] solvable [-3] -- rule [3] solvable [-2] -- rule [0] solvable [-1] -- rule [0] solvable [0] -- rule [0] solvable [1] -- rule [0] solvable [2] -- rule [0] solvable [3] -- rule [1] solvable [4] -- rule [0] solvable [5] -- rule [0] solvable [6] -- rule [0] solvable [7] -- rule [2] solvable [8] -- rule [2] solvable [9] -- rule [0] solvable [10] -- rule [0] solvable [11] -- rule [0] solvable [12] -- rule [0] ----- propagate end-----
Results
>!> Solution #1: >!> install A-1.0-1.noarch[test] >!> install Z-1.0-1.noarch[test] >!> install E-1.0-1.noarch[test] >!> installs=3, upgrades=0, uninstalls=0
Problem case
Has to be described.